4283. Степан и пары

Степана заинтересовал наибольший общий делитель пары чисел, а именно НОД(x, y). По целому числу n Степан хочет узнать, сколько существует таких пар целых чисел (i, j), что 1 ≤ i, j ≤ n и выполняется равенство i = НОД(i, j).

Вход. Одно целое число n (1 ≤ n ≤ 10⁶).

Выход. Выведите количество искомых пар целых чисел.

Пример входа	Пример выхода
4	8

РЕШЕНИЕ

теория чисел

Анализ алгоритма

Зафиксируем j (например j = 12) и найдем количество таких i, что i = НОД(i, 12). Найдем значения i, удовлетворяющие этому равенству. Ими будут i = 1, 2, 3, 4, 6, 12. То есть любое i, являющееся делителем 12, удовлетворяет равенству i = НОД(i, 12).

Количество таких i для которых i = НОД(i, j), равно количеству делителей d(j) числа j. Поскольку 1 ≤ j ≤ n, то остается найти количество всех делителей чисел от 1 до n. То есть следует найти сумму d(1) + d(2) + … + d(n). Поскольку вычисление d(n) требует факторизации числа n, то непосредственное вычисление указанной суммы потребует времени O(n).

Посмотрим на сумму делителей по-другому. Среди делителей чисел от 1 до n единица будет встречаться раз, двойка раз и так далее (делитель i будет встречаться раз). Количество искомых пар целых чисел равно

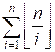
Указанную сумму можно найти за время O(n).

Пример

При n = 6 имеем следующие пары:

Количество пар равно 6 / 1 + 6 / 2 + 6 / 3 + 6 / 4 + 6 / 5 + 6 / 6 =

= 6 + 3 + 2 + 1 + 1 + 1 = 14

Реализация алгоритма

Читаем значение n.

scanf("%d",&n);

Вычисляем ответ по формуле и выводим его.

s = 0;

for(i = 1; i <= n; i++)

s += n / i;

printf("%d\n",s);

Java реализация

import java.util.*;

class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int s = 0;

for(int i = 1; i <= n; i++)

s += n / i;

System.out.println(s);

con.close();

}

}

Python реализация

Читаем значение n.

n = int(input())

Вычисляем ответ по формуле и выводим его.

s = 0

for i in range(1,n+1):

s += n // i

print(s)